Zadanie nr 8442156
Ze zbioru liczb 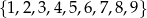 losujemy kolejno bez zwracania trzy liczby, zapisujemy je w kolejności losowania i tworzymy liczbę trzycyfrową w taki sposób, że pierwsza wylosowana liczba jest cyfrą setek, druga jest cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba trzycyfrowa jest podzielna przez 4. Wynik przedstaw w postaci ułamka nieskracalnego.
losujemy kolejno bez zwracania trzy liczby, zapisujemy je w kolejności losowania i tworzymy liczbę trzycyfrową w taki sposób, że pierwsza wylosowana liczba jest cyfrą setek, druga jest cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba trzycyfrowa jest podzielna przez 4. Wynik przedstaw w postaci ułamka nieskracalnego.
Rozwiązanie
Wszystkich liczb trzycyfrowych zapisanych przy pomocy różnych cyfr niezerowych jest
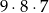
(każdą z cyfr możemy wybrać na 9 sposobów). Wypiszmy teraz wszystkie możliwe końcówki takich liczb, które dzielą się przez 4:
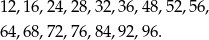
Do każdej z tych 16 końcówek możemy na 7 sposobów dobrać pierwszą cyfrę, więc interesujące nas prawdopodobieństwo jest równe
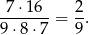
Odpowiedź: