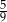Zadanie nr 8960555
Ze zbioru liczb 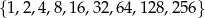 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 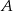 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
Rozwiązanie
Każdą z liczb możemy wybrać na 9 sposobów, więc
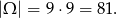
Zauważmy teraz, że są trzy rodzaje zdarzeń elementarnych 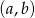 : takie, w których
: takie, w których 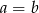 , takie w których
, takie w których 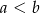 i wreszcie takie, w których
i wreszcie takie, w których 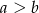 . Zdarzeń pierwszego typu jest 9:
. Zdarzeń pierwszego typu jest 9:
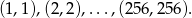
Zdarzeń drugiego rodzaju jest dokładnie tyle samo, co zdarzeń trzeciego rodzaju (bo każdej parze 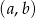 , w której
, w której 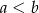 odpowiada dokładnie jedna para trzeciego rodzaju:
odpowiada dokładnie jedna para trzeciego rodzaju: 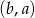 ). Jest więc
). Jest więc 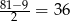 par każdego z tych dwóch rodzajów.
par każdego z tych dwóch rodzajów.
Zauważmy teraz, że dane liczby to kolejne potęgi dwójki
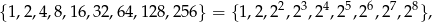
więc wylosowana para 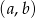 spełnia warunki zadania (czyli
spełnia warunki zadania (czyli  dzieli się przez
dzieli się przez 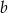 ) wtedy i tylko wtedy, gdy
) wtedy i tylko wtedy, gdy 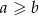 . Jak już wiemy, jest
. Jak już wiemy, jest
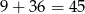
takich par i interesujące nas prawdopodobieństwo wynosi
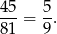
Odpowiedź: