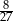/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Różne

Zadanie nr 3038295

Ze zbioru 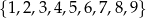{1,2,3,4,5,6,7 ,8 ,9} losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.

Wersja PDF

Rozwiązanie

Wszystkich zdarzeń elementarnych jest

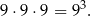
3 9⋅9 ⋅9 = 9 .

Sposób I

Zastanówmy się teraz ile jest zdarzeń sprzyjających. Miejsca dla dwóch równych liczb możemy wybrać na

( ) 3 2 = 3

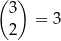
sposoby. Potem na 9 sposobów możemy wybrać te liczby i na koniec na 8 sposobów wybieramy trzecią liczbę różną od dwóch pozostałych. W sumie jest więc

3⋅9 ⋅8

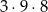
zdarzeń sprzyjających i interesujące nas prawdopodobieństwo jest równe

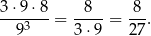
3⋅9 ⋅8 8 8 ---3---= ---- = ---. 9 3⋅ 9 2 7

Sposób II

Zamiast liczyć zdarzenia sprzyjające zastanówmy się nad zdarzeniami przeciwnymi. Są to zdarzenia, w których wszystkie trzy liczby są różne – jest ich

9 ⋅8 ⋅7,

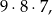
oraz takie, w których wszystkie trzy liczby są takie same – takich zdarzeń jest 9. Interesujące nas prawdopodobieństwo jest więc równe

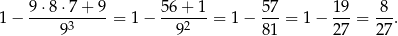
9⋅8 ⋅7 + 9 56 + 1 57 1 9 8 1 − -----------= 1− -------= 1 − ---= 1 − --- = ---. 93 92 81 2 7 2 7

 
Odpowiedź: 287

Wersja PDF