Zadanie nr 5249450
Ze zbioru liczb 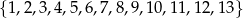 losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.
losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.
Rozwiązanie
Wszystkich zdarzeń elementarnych jest
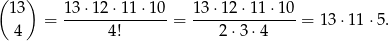
Wypiszmy wszystkie pary liczb, które w sumie dają 14.
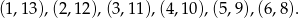
Jest jeszcze liczba 7, która nie ma pary (bo losujemy bez zwracania).
Sposób I
O zdarzeniach sprzyjających myślimy następująco: musimy wybrać jedną z powyższych par, a potem musimy dobrać jeszcze dwie liczby tak, aby nie były z jednej pary.
Jedną parę możemy wybrać na 6 sposobów. Po wybraniu tej pary pozostaje 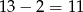 liczb i z nich musimy wybrać jeszcze dwie. Dwie pozostałe liczby możemy wybrać na
liczb i z nich musimy wybrać jeszcze dwie. Dwie pozostałe liczby możemy wybrać na
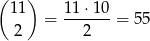
sposobów. Od tych 55 możliwych par musimy jednak odjąć 5 par, w których suma jest równa 14. W sumie 3 i 4 liczbę możemy więc wybrać na 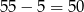 sposobów. Jest więc
sposobów. Jest więc
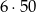
zdarzeń sprzyjających i prawdopodobieństwo jest równe
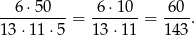
Sposób II
O zdarzeniach sprzyjających myślimy następująco: musimy wybrać jedną z powyższych par, a potem musimy dobrać jeszcze dwie liczby tak, aby nie były z jednej pary.
Jedną parę możemy wybrać na 6 sposobów. Gdy para ta jest ustalona to możliwe są dwie sytuacje: albo jedną z pozostałych liczb jest 7, albo nie. Jeżeli jest 7 wśród wylosowanych liczb to czwarta liczba może być którąkolwiek z pozostałych 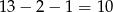 liczb. Jest więc
liczb. Jest więc
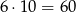
zdarzeń tego typu.
Jeżeli natomiast wśród wylosowanych liczb nie ma 7, to pozostałe dwie liczby wybieramy spośród 5 par tak, aby dwie liczby nie były z jednej pary. W takim razie trzecią liczbę wybieramy dowolnie spośród 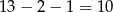 liczb (odejmujemy wybraną na początku parę i 7), a czwartą liczbę wybieramy spośród
liczb (odejmujemy wybraną na początku parę i 7), a czwartą liczbę wybieramy spośród 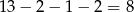 liczb (odejmujemy pierwszą parę, 7-kę, oraz parę trzeciej liczby). Teraz bardzo łatwo popełnić błąd – zauważmy, że przy takim sposobie liczenia, np. czwórkę
liczb (odejmujemy pierwszą parę, 7-kę, oraz parę trzeciej liczby). Teraz bardzo łatwo popełnić błąd – zauważmy, że przy takim sposobie liczenia, np. czwórkę 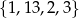 policzyliśmy dwukrotnie: jako
policzyliśmy dwukrotnie: jako 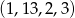 i
i 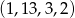 ! W takim razie zdarzeń bez 7-ki jest
! W takim razie zdarzeń bez 7-ki jest
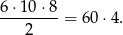
Zdarzenia bez 7-ki mogliśmy też policzyć inaczej: parę z sumą równą 14 możemy wybrać na 6 sposobów, potem wybieramy dwie pary, z których będą pochodzić dwie pozostałe liczby – możemy to zrobić na
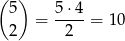
sposobów. Na koniec musimy jeszcze uwzględnić, że w każdej z tych dwóch ostatnich par mamy możliwość wyboru jednej z dwóch liczb. Daje to w sumie
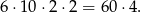
możliwości.
Prawdopodobieństwo jest więc równe
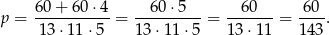
Sposób III
Tym razem, zamiast obliczać prawdopodobieństwo opisanego zdarzenia 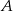 , obliczymy prawdopodobieństwo zdarzenia przeciwnego
, obliczymy prawdopodobieństwo zdarzenia przeciwnego 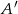 . Są dwa rodzaje zdarzeń sprzyjających zdarzeniu
. Są dwa rodzaje zdarzeń sprzyjających zdarzeniu 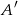 : albo nie ma żadnej pary z sumą równą 14, albo takie pary są dwie.
: albo nie ma żadnej pary z sumą równą 14, albo takie pary są dwie.
Łatwo obliczyć liczbę zdarzeń z dwoma parami z sumą równą 14 – jest ich tyle, ile możliwości wybrania 2 par spośród 6 par wypisanych powyżej. Jest więc
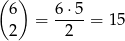
zdarzeń tego typu.
Jeżeli natomiast nie ma żadnej pary liczb z sumą równą 14, to każda z liczb musi pochodzić z innej z wypisanych par, lub może być też 7-ką.
Jeżeli wśród wybranych liczb jest 7, to aby wybrać pozostałe trzy liczby wybieramy 3 pary, z których będą pochodzić, możemy to zrobić na
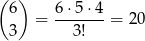
sposobów. Ponadto w każdej z 3 wybranych par możemy wybrać jedną z dwóch liczb jest więc
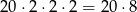
takich par.
Jeżeli wreszcie wśród wybranych liczb nie ma 7-ki, to liczby pochodzą z 4 różnych par, co możemy wybrać na
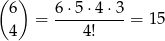
sposobów. W każdej parze mamy możliwość wyboru jednej z 2 liczb. Jest więc
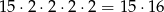
takich zdarzeń.
Prawdopodobieństwo jest więc równe.
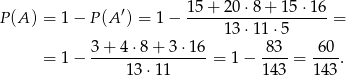
Sposób IV
Tym razem będziemy uwzględniać kolejność w jakiej losowane są liczby, czyli za zdarzenia elementarne przyjmiemy czwórki 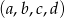 wylosowanych liczb. Mamy zatem
wylosowanych liczb. Mamy zatem
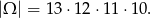
Liczymy ile jest zdarzeń sprzyjających.
Najpierw zdarzenia w których jest 7. Do tej siódemki musimy dobrać parę liczb z sumą równą 14 – możemy to zrobić na 6 sposobów, a potem jeszcze jedną dowolną liczbę spośród pozostałych 10 liczb. Na koniec musimy ustalić kolejność wybranych liczb, co możemy zrobić na 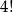 sposobów. W sumie jest więc
sposobów. W sumie jest więc
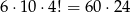
takich zdarzeń.
Teraz policzmy ile jest zdarzeń bez 7-ki. Musimy wybrać dwie liczby z sumą równą 14 – możemy to zrobić na 6 sposobów, potem musimy jeszcze dobrać dwie liczby, których suma nie jest równa 14. Łatwo tu popełnić błąd, nie możemy liczyć tak: wybieramy liczbę spośród pozostałych 10, a potem ostatnią liczbę możemy wybrać na 8 sposobów – przy takim sposobie liczenia każdą parę liczymy podwójnie.
W takim razie liczmy ostrożniej, aby wybrać dwie liczby, których suma nie jest równa 14, wybieramy dwie pary, z których będą pochodzić te liczby – możemy to zrobić na
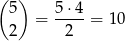
sposobów, a potem z każdej pary wybieramy jedną z dwóch liczb w tej parze. W sumie jest więc
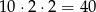
możliwości wybrania dwóch liczb, których suma nie jest równa 14. Na koniec możemy 4 wybrane liczby dowolnie permutować, więc jest w sumie
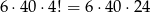
zdarzeń bez 7-ki. Prawdopodobieństwo jest więc równe
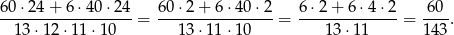
Odpowiedź: