/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Różne

Zadanie nr 5487467

Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest o 85 większa od drugiej. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

Wersja PDF

Rozwiązanie

Wszystkich liczb dwucyfrowych jest 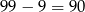99− 9 = 90 , więc parę różnych liczb 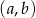(a,b) możemy wylosować na

90 ⋅89

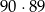
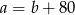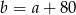sposobów. Jeżeli a = b + 80 lub b = a+ 80 , to mamy 10 zdarzeń sprzyjających

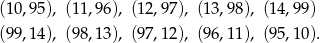
(10,95), (11,96), (12,97), (13,98), (14,99) (99,14), (98,13), (97,12), (96,11), (95,10).

Interesujące nas prawdopodobieństwo jest więc równe

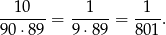
--10--- -1---- -1-- 90⋅ 89 = 9⋅89 = 801 .

 
Odpowiedź: -1- 801

Wersja PDF