/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Różne

Zadanie nr 7410683

Ze zbioru siedmiu liczb naturalnych 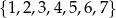{ 1,2,3,4,5,6,7} losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.

Wersja PDF

Rozwiązanie

Sposób I

Nieuporządkowaną parę liczb z danego zbioru możemy wybrać na

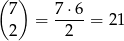
( 7) 7 ⋅6 = ---- = 2 1 2 2

sposobów. Są 4 zdarzenia sprzyjające:

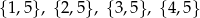
{1 ,5}, { 2,5}, {3,5}, {4,5}

więc interesujące nas prawdopodobieństwo jest równe

4-. 21

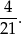
Sposób II

Tym razem na zdarzenia sprzyjające patrzymy jak na uporządkowane pary 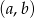(a,b) wybranych liczb. Takich par jest

7 ⋅6 = 42.

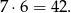
Jest ponadto 8 zdarzeń sprzyjających

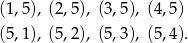
(1,5), (2,5), (3 ,5), (4,5) (5,1), (5,2), (5 ,3), (5,4).

Interesujące nas prawdopodobieństwo jest więc równe

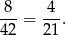
8-- -4- 42 = 2 1.

 
Odpowiedź: -4 21

Wersja PDF