Zadanie nr 7627215
Ze zbioru liczb 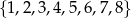 wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
Rozwiązanie
Losujemy cztery liczby z ośmiu, więc
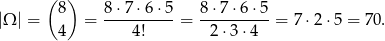
Jeżeli oznaczymy przez 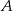 zdarzenie polegające na tym, że najmniejsza z wylosowanych liczb jest 3, a przez
zdarzenie polegające na tym, że najmniejsza z wylosowanych liczb jest 3, a przez 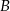 zdarzenie, że największa z liczb to 7, to musimy obliczyć
zdarzenie, że największa z liczb to 7, to musimy obliczyć
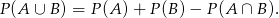
W zdarzeniach sprzyjających zdarzeniu 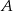 musimy do liczby 3 dobrać trzy liczby ze zbioru
musimy do liczby 3 dobrać trzy liczby ze zbioru 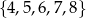 , więc jest
, więc jest
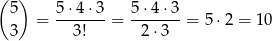
zdarzeń sprzyjających zdarzeniu 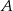 . Analogicznie jest
. Analogicznie jest
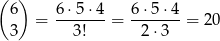
zdarzeń sprzyjających 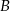 .
.
W przypadku zdarzenia 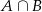 do skrajnych liczb: 3 i 7 musimy dobrać dwie liczby ze zbioru
do skrajnych liczb: 3 i 7 musimy dobrać dwie liczby ze zbioru 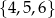 . Są więc
. Są więc
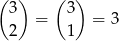
zdarzenia sprzyjające temu zdarzeniu i interesujące nas prawdopodobieństwo jest równe
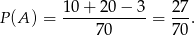
Odpowiedź: