/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Różne

Zadanie nr 9073583

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru ośmiu liczb naturalnych 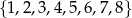{1,2,3,4,5 ,6 ,7,8} losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.

Rozwiązanie

Sposób I

Nieuporządkowaną parę liczb z danego zbioru możemy wybrać na

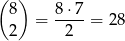
( 8) 8 ⋅7 = ---- = 2 8 2 2

sposobów. Jest 5 zdarzeń sprzyjających:

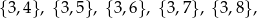
{ 3,4}, {3,5}, {3,6} , {3,7 }, { 3,8},

więc interesujące nas prawdopodobieństwo jest równe

5-. 28

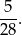
Sposób II

Tym razem na zdarzenia sprzyjające patrzymy jak na uporządkowane pary 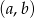(a,b) wybranych liczb. Takich par jest

8 ⋅7 = 56.

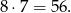
Jest ponadto 10 zdarzeń sprzyjających

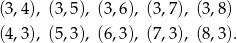
(3,4), (3,5 ), (3,6), (3,7), (3,8) (4,3), (5,3 ), (6,3), (7,3), (8,3).

Interesujące nas prawdopodobieństwo jest więc równe

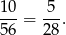
10- -5- 56 = 2 8.

 
Odpowiedź: -5 28

Wersja PDF