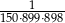Zadanie nr 9115095
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy kolejno trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 304.
Rozwiązanie
Wszystkich liczb trzycyfrowych jest 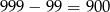 , więc trójkę różnych liczb
, więc trójkę różnych liczb 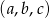 możemy wylosować na
możemy wylosować na
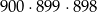
sposobów. Jeżeli suma liczb 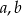 i
i  ma być równa 304, to mamy 6 zdarzeń sprzyjających
ma być równa 304, to mamy 6 zdarzeń sprzyjających
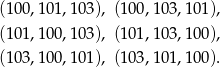
Interesujące nas prawdopodobieństwo jest więc równe
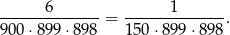
Odpowiedź: