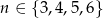/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Różne

Zadanie nr 9915946

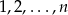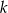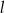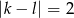Ze zbioru 1,2,...,n losujemy kolejno bez zwracania 2 liczby k i l . Dla jakich wartości n prawdopodobieństwo tego, że |k− l| = 2 jest większe od 14 ?

Wersja PDF

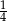Rozwiązanie

Łatwo sprawdzić, że dla 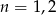n = 1,2 prawdopodobieństwo interesującego nas zdarzenia jest równe 0, więc możemy założyć, że n ≥ 3 .

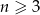Sposób I

Powiedzmy, że za zdarzenia elementarne przyjmujemy uporządkowane pary wylosowanych liczb. Mamy zatem

|Ω | = n(n − 1).

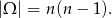
Warunek 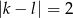|k − l| = 2 oznacza, że liczby są odległe o 2. Powinno być jasne, że liczba możliwości wyboru 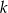k dla ustalonego 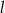l zależy od tego, czy 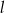l jest blisko końca. Dokładniej rzecz biorąc, jeżeli 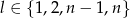l ∈ {1,2,n − 1,n } to istnieje tylko jedno 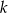k . W przeciwnym przypadku są dwie możliwe wartości 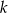k . Zatem jest

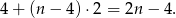
4 + (n − 4) ⋅2 = 2n − 4.

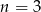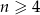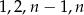zdarzeń sprzyjających. Tutaj jest delikatne miejsce, bo przypadek n = 3 lepiej rozważyć osobno (zrobimy to na koniec) – możemy więc założyć, że n ≥ 4 i 1,2,n − 1,n to rzeczywiście cztery różne liczby.

Zatem prawdopodobieństwo wynosi

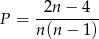
P = -2n-−-4-- n(n − 1 )

i mamy nierówność

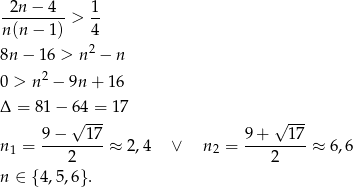
-2n-−-4-- 1- n(n − 1 ) > 4 2 8n − 16 > n − n 0 > n2 − 9n + 1 6 Δ = 81− 64 = 17 √ --- √ --- n1 = 9−---1-7-≈ 2,4 ∨ n2 = 9-+---17-≈ 6,6 2 2 n ∈ {4,5 ,6 }.

Pozostało sprawdzić przypadek 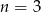n = 3 . Mamy dwa zdarzenia sprzyjające: 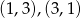(1,3),(3 ,1 ) , czyli prawdopodobieństwo wynosi

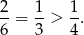
2- 1- 1- 6 = 3 > 4.

Sposób II

Tym razem za zdarzenia elementarne przyjmijmy nieuporządkowane pary 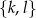{k,l} wylosowanych liczb. Mamy więc

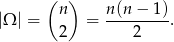
( ) n n(n-−-1)- |Ω | = 2 = 2 .

Zauważmy teraz, że jest 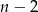n − 2 nieuporządkowanych par spełniających warunek |k− l| = 2 :

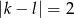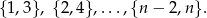
{1,3}, {2,4} ,...,{n − 2,n} .

Zatem prawdopodobieństwo otrzymania takiej pary jest równe

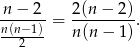
-n-−-2- = 2-(n−--2). n(n−-1) n (n− 1) 2

Pozostało rozwiązać nierówność

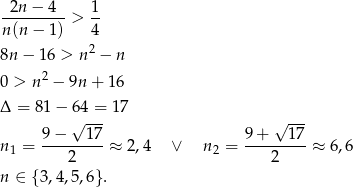
-2n-−-4-- 1- n(n − 1 ) > 4 2 8n − 16 > n − n 0 > n2 − 9n + 1 6 Δ = 81− 64 = 17 √ --- √ --- n1 = 9−---1-7-≈ 2,4 ∨ n2 = 9-+---17-≈ 6,6 2 2 n ∈ {3,4 ,5 ,6}.

 
Odpowiedź: n ∈ { 3,4,5,6}

Wersja PDF