/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 1147538

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 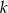k równanie 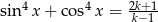4 4 2k+-1 sin x + co s x = k−1 ma rozwiązanie?

Rozwiązanie

Ze względu na ułamek z prawej strony równości musimy założyć, że 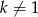k ⁄= 1 .

Sposób I

Przekształćmy lewą stronę równania

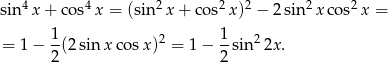
sin 4x + cos4 x = (sin2x + co s2x)2 − 2sin2 xco s2x = 1- 2 1- 2 = 1 − 2(2sin xco sx) = 1 − 2 sin 2x.

Możemy teraz następująco zapisać podane równanie

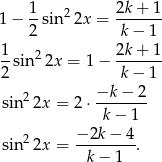
1− 1-sin 22x = 2k+--1- 2 k − 1 1 2 2k+ 1 --sin 2x = 1− ------- 2 k − 1 sin22x = 2 ⋅ −k-−-2 k− 1 − 2k − 4 sin22x = ---------. k− 1

Równanie to ma rozwiązania wtedy i tylko wtedy, gdy prawa strona jest w przedziale 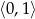⟨0 ,1⟩ .

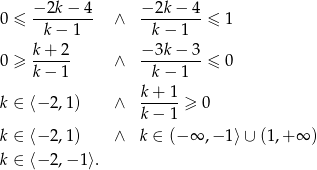
− 2k− 4 −2k − 4 0 ≤ --------- ∧ --------≤ 1 k − 1 k − 1 0 ≥ k+--2- ∧ −3k-−-3-≤ 0 k− 1 k − 1 k+ 1 k ∈ ⟨− 2,1) ∧ -----≥ 0 k− 1 k ∈ ⟨− 2,1) ∧ k ∈ (− ∞ ,− 1⟩ ∪ (1,+ ∞ ) k ∈ ⟨− 2,− 1⟩.

Sposób II

Przekształćmy lewą stronę równania

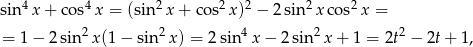
4 4 2 2 2 2 2 sin x + cos x = (sin x + co s x) − 2sin xco s x = = 1 − 2 sin 2x(1 − sin2 x) = 2 sin 4x − 2sin2 x+ 1 = 2t2 − 2t+ 1,

gdzie podstawiliśmy 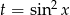t = sin 2x . Spróbujmy ustalić jakie wartości przyjmuje parabola 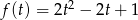f(t) = 2t2 − 2t+ 1 na przedziale 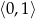⟨0 ,1⟩ (tak zmienia się 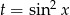t = sin 2x ). Ponieważ jej wierzchołek znajduje się w punkcie

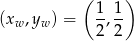
( ) 1-1- (xw ,yw ) = 2,2

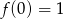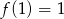oraz f(0) = 1 i f(1) = 1 , możliwe wartości 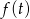f (t) to przedział 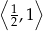⟨ ⟩ 1 2,1 . Podane równanie będzie więc miało rozwiązanie wtedy i tylko wtedy gdy prawa strona równania będzie zawarta w tym przedziale.

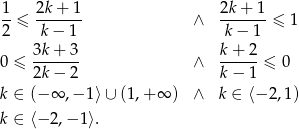
1- 2k-+-1- 2k+--1- 2 ≤ k − 1 ∧ k − 1 ≤ 1 3k + 3 k+ 2 0 ≤ ------- ∧ -----≤ 0 2k − 2 k− 1 k ∈ (− ∞ ,− 1⟩ ∪ (1,+ ∞ ) ∧ k ∈ ⟨− 2,1) k ∈ ⟨− 2 ,− 1 ⟩.

Sposób III

Korzystamy z łatwych do uzasadnienia nierówności

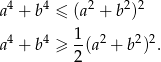
a4 + b4 ≤ (a2 + b2)2 a4 + b4 ≥ 1-(a2 + b 2)2. 2

Mamy zatem

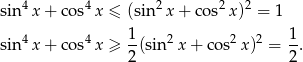
4 4 2 2 2 sin x+ cos x ≤ (sin x + cos x) = 1 4 4 1- 2 2 2 1- sin x+ cos x ≥ 2(sin x+ cos x ) = 2.

Ponadto funkcja 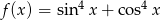f(x) = sin 4x + cos4x jest ciągła i 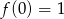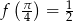f(0) = 1 , ( ) f π- = 1 4 2 . To oznacza, że jej zbiorem wartości jest przedział 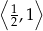⟨1 ⟩ 2 ,1 i dane równanie ma rozwiązanie wtedy i tylko wtedy, gdy jego prawa strona jest w przedziale 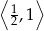⟨1 ⟩ 2,1 . Nierówność tę rozwiązujemy tak samo jak w poprzednim sposobie.  
Odpowiedź: k ∈ ⟨− 2,− 1⟩

Wersja PDF