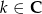Zadanie nr 1203611
Rozwiąż równanie 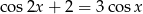 .
.
Rozwiązanie
Korzystamy ze wzoru
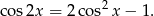
Mamy zatem
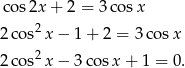
Podstawiamy teraz 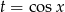 .
.
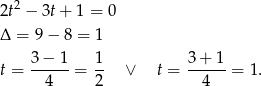
Zatem
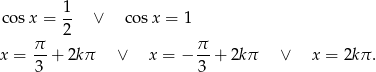
Odpowiedź: 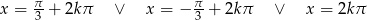 , gdzie
, gdzie 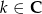
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 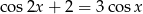 .
.
Korzystamy ze wzoru
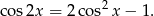
Mamy zatem
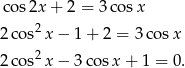
Podstawiamy teraz 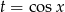 .
.
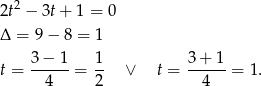
Zatem
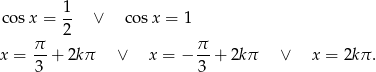
Odpowiedź: 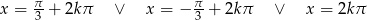 , gdzie
, gdzie