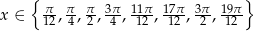/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 2151326

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 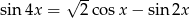√ -- sin4x = 2 cosx − sin 2x w przedziale ⟨0 ,2π⟩ .

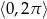Rozwiązanie

Korzystamy ze wzorów na sumę sinusów.

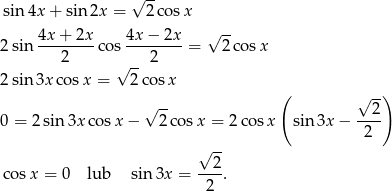
√ -- sin 4x + sin2x = 2co sx 4x-+-2x- 4x-−-2x- √ -- 2 sin 2 co s 2 = 2 cosx √ -- 2 sin 3x cosx = 2co sx ( ) √ -- √ 2- 0 = 2 sin 3x cos x− 2cos x = 2 cosx sin3x − ---- 2 √ -- co sx = 0 lub sin 3x = --2. 2

Pierwsze równanie ma dwa rozwiązania 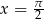π x = 2- i 3π x = -2- .

PIC

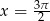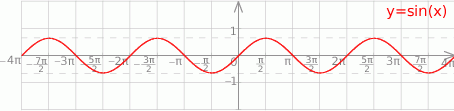
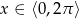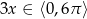W przypadku drugiego równania łatwo o pomyłkę, bo wprawdzie x ∈ ⟨0 ,2π⟩ , ale 3x ∈ ⟨0,6 π⟩ . Mamy zatem

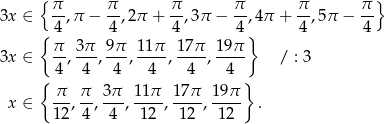
{ } 3x ∈ π-,π − π-,2π + π-,3π − π,4 π + π-,5π − π- { 4 4 4 4} 4 4 π- 3π- 9π- 1-1π 17π- 19π- 3x ∈ 4 , 4 , 4 , 4 , 4 , 4 / : 3 { } x ∈ π-, π, 3π-, 11π-, 17π-, 19π . 12 4 4 12 12 1 2

Dane równanie ma więc 8 rozwiązań w przedziale 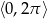⟨0,2π ⟩

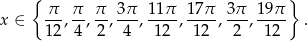
{ } π-- π- π- 3π- 11π- 17π- 3π- 19π- x ∈ 12 ,4 ,2 , 4 , 12 , 12 , 2 , 12 .

 
Odpowiedź: { } π- π- π- 3π--11π 17π 3π-19π x ∈ 12,4 ,2, 4 , 12 , 12 ,2 , 12

Wersja PDF