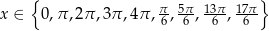/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 2459299

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 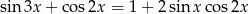sin3x + cos2x = 1+ 2sin xco s2x dla x ∈ ⟨0,4π ⟩ .

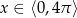Rozwiązanie

Na początek rozpiszmy 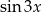sin3x ze wzoru na sinus sumy.

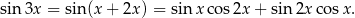
sin 3x = sin(x + 2x ) = sinx cos 2x+ sin 2x cos x.

Dane równanie przyjmuje więc postać

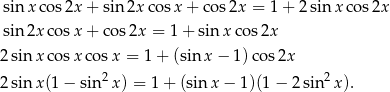
sin x cos2x + sin 2xco sx + cos 2x = 1 + 2 sin x cos2x sin 2x cosx + co s2x = 1+ sin xco s2x 2 sin x cosx cos x = 1 + (sinx − 1) cos2x 2 sin x(1 − sin2x ) = 1+ (sin x − 1)(1 − 2 sin 2x).

Widać teraz, że możemy podstawić 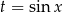t = sin x .

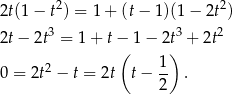
2t(1− t2) = 1+ (t− 1)(1 − 2t2) 3 3 2 2t− 2t = 1+ t− 1 − 2t + 2t ( 1) 0 = 2t2 − t = 2t t− -- . 2

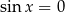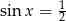Stąd sin x = 0 lub 1 sin x = 2 . Szkicujemy sinusa.

PIC

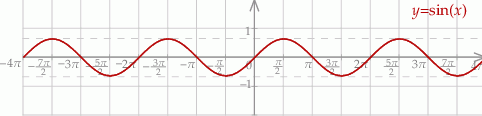
Z wykresu odczytujemy rozwiązania.

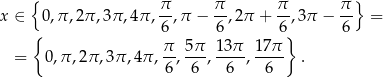
{ π π π π } x ∈ 0,π ,2π ,3π ,4π,--,π − --,2π + --,3π − -- = { 6 6 6} 6 = 0,π,2 π,3π ,4π , π-, 5π-, 13-π, 17π . 6 6 6 6

 
Odpowiedź: { } x ∈ 0,π ,2π,3π ,4π , π-, 5π, 13π, 17π 6 6 6 6

Wersja PDF