Zadanie nr 2489029
Rozwiąż równanie 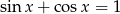 .
.
Rozwiązanie
Sposób I
Korzystamy ze wzoru 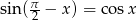 i ze wzoru na sumę sinusów.
i ze wzoru na sumę sinusów.
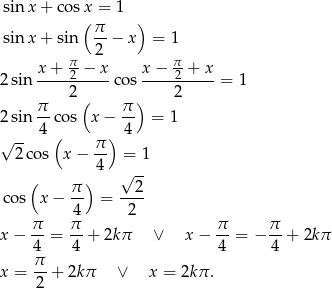
Sposób II
Tym razem skorzystamy ze wzoru na cosinus różnicy.
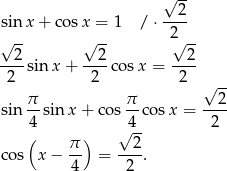
i jesteśmy w tej samej sytuacji co w poprzednim sposobie.
Sposób III
Podnieśmy podane równanie do kwadratu.
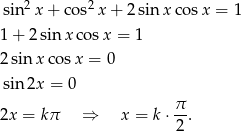
Po drodze podnieśliśmy równanie do kwadratu, więc trzeba sprawdzić otrzymane rozwiązania (bo mogliśmy jakieś dołożyć, jak np. po podniesieniu 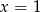 do kwadratu). Sprawdzając, mamy cztery możliwości w zalezności od reszty z dzielnia
do kwadratu). Sprawdzając, mamy cztery możliwości w zalezności od reszty z dzielnia 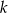 przez 4. Łatwo sprawdzić, że rozwiązanie otrzymujemy tylko dla
przez 4. Łatwo sprawdzić, że rozwiązanie otrzymujemy tylko dla 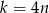 i
i 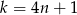 . W pozostałych przypadkach, czyli
. W pozostałych przypadkach, czyli 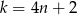 i
i 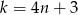 mamy
mamy 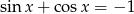 .
.
Sposób IV
Podobnie jak poprzednio podnosimy równanie do kwadratu i mamy
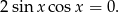
Zatem 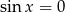 lub
lub 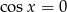 . Mamy wtedy odpowiednio
. Mamy wtedy odpowiednio
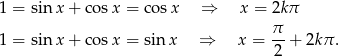
Sposób V
Tym razem zamienimy 1 na 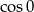 .
.
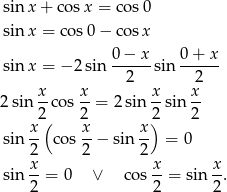
Z pierwszego równania mamy
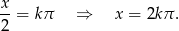
W drugim możemy założyć, że obie strony są niezerowe (bo taki przypadek właśnie rozważyliśmy) i mamy
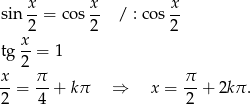
Sposób VI
Tym razem skorzystamy ze wzoru na 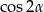 .
.
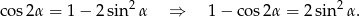
Mamy zatem
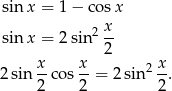
i jesteśmy w takiej samej sytuacji jak w poprzednim sposobie.
Odpowiedź: 

