/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 2577690

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 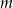m równanie 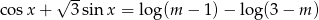√ -- co sx + 3 sin x = log(m − 1) − log(3 − m ) ma rozwiązania.

Rozwiązanie

Sprawdźmy najpierw kiedy prawa strona ma sens

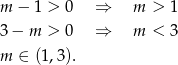
m − 1 > 0 ⇒ m > 1 3− m > 0 ⇒ m < 3 m ∈ (1 ,3).

Przekształćmy podane równanie korzystając ze wzoru 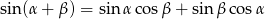sin (α+ β) = sinα cos β + sinβ cos α .

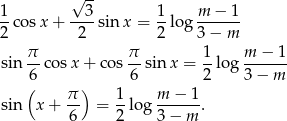
√ -- 1-cos x+ --3-sin x = 1-lo g m-−-1 2 2 2 3 − m π π 1 m − 1 sin 6-co sx + cos 6-sin x = 2-log 3−--m- ( ) sin x + π- = 1-log m-−--1. 6 2 3− m

Aby równanie to miało rozwiązanie prawa strona musi być w przedziale 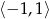⟨− 1,1⟩ .

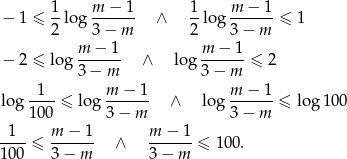
− 1 ≤ 1-log m-−--1 ∧ 1-log m-−-1-≤ 1 2 3 − m 2 3− m m − 1 m − 1 − 2 ≤ log ------ ∧ log ------≤ 2 3 − m 3− m log -1-- ≤ log m-−-1- ∧ log m-−-1-≤ log1 00 10 0 3− m 3− m 1 m − 1 m − 1 ---- ≤ ------ ∧ ------≤ 100. 10 0 3 − m 3− m

Ponieważ z założenia 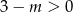3 − m > 0 możemy pomnożyć przez mianownik.

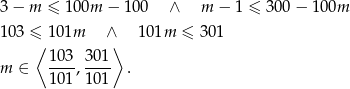
3 − m ≤ 100m − 100 ∧ m − 1 ≤ 3 00− 100m 103 ≤⟨ 101m ∧⟩ 101m ≤ 30 1 103 301 m ∈ ---, ---- . 101 101

 
Odpowiedź: ⟨ 103 301⟩ m ∈ 101, 101-

Wersja PDF