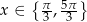/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 2689973

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 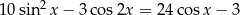2 10sin x− 3co s2x = 2 4cos x− 3 dla x ∈ ⟨0,2π ⟩ .

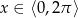Rozwiązanie

Zapiszemy dane równanie tak, aby zawierało tylko 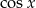cosx . Skorzystamy po drodze ze wzorów

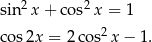
2 2 sin x + cos x = 1 cos2x = 2co s2x − 1.

Przekształcamy równanie i podstawiamy 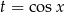t = cos x .

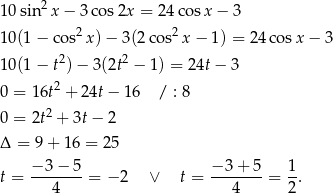
10 sin 2x − 3 cos2x = 24co sx − 3 10(1 − co s2 x)− 3(2c os2x − 1) = 2 4cos x− 3 2 2 10(1 − t )− 3(2t − 1) = 24t− 3 0 = 16t2 + 24t − 16 / : 8 2 0 = 2t + 3t− 2 Δ = 9+ 16 = 25 t = −-3-−-5 = − 2 ∨ t = −-3-+-5 = 1. 4 4 2

Ponieważ 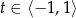t ∈ ⟨− 1,1⟩ , mamy stąd 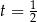t = 12 , czyli

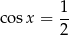
cos x = 1- 2

Szkicujemy cosinusa.

PIC

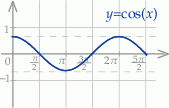
Z wykresu odczytujemy rozwiązania

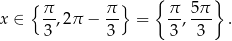
{ } { } x ∈ π-,2π − π- = π-, 5π . 3 3 3 3

 
Odpowiedź: { } x ∈ π, 5π-- 3 3

Wersja PDF