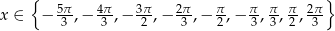Zadanie nr 2758474
Rozwiąż równanie 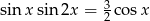 w przedziale
w przedziale 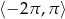 .
.
Rozwiązanie
Korzystamy ze wzoru
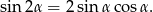
Liczymy
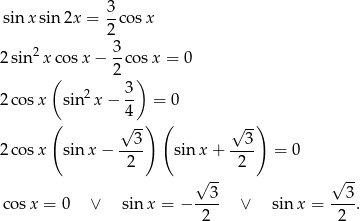
Stąd
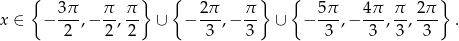
Odpowiedź: 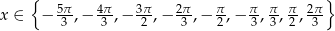
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 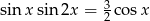 w przedziale
w przedziale 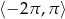 .
.
Korzystamy ze wzoru
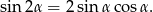
Liczymy
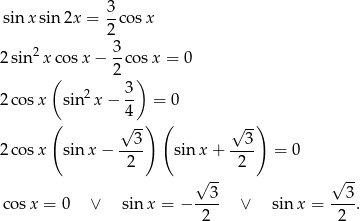
Stąd
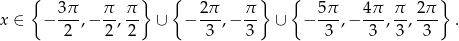
Odpowiedź: