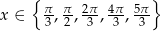Zadanie nr 3124116
Rozwiąż równanie: 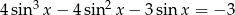 w przedziale
w przedziale 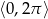 .
.
Rozwiązanie
Przekształcamy dane równanie
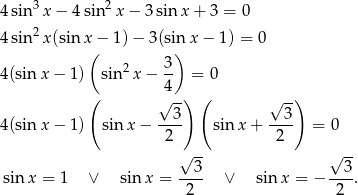
Teraz szkicujemy sinusa.
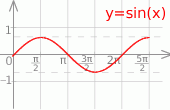
Rozwiązaniami równania są liczby
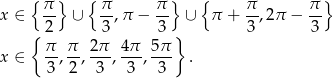
Odpowiedź: 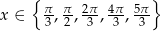
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie: 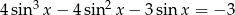 w przedziale
w przedziale 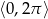 .
.
Przekształcamy dane równanie
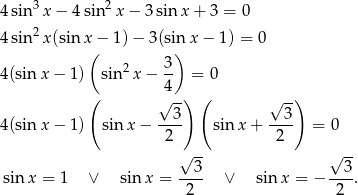
Teraz szkicujemy sinusa.

Rozwiązaniami równania są liczby
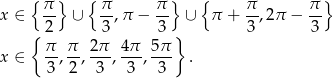
Odpowiedź: