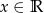Zadanie nr 3877970
Rozwiąż równanie 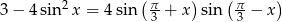 .
.
Rozwiązanie
Przekształcamy podane równanie korzystając ze wzorów na sinus sumy i sinus różnicy.
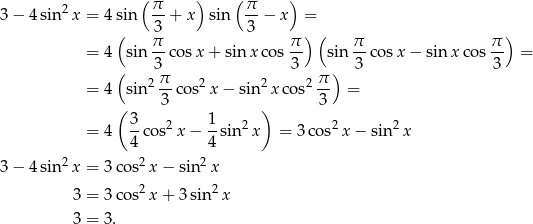
Dane równanie jest więc tożsamością, czyli jest spełnione przez dowolną liczbę rzeczywistą  .
.
Odpowiedź: 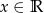
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 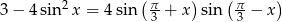 .
.
Przekształcamy podane równanie korzystając ze wzorów na sinus sumy i sinus różnicy.
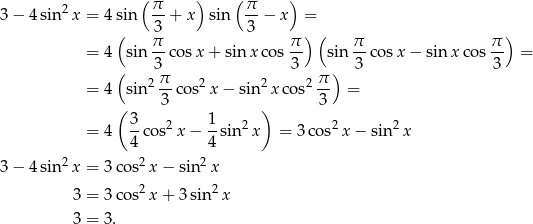
Dane równanie jest więc tożsamością, czyli jest spełnione przez dowolną liczbę rzeczywistą  .
.
Odpowiedź: