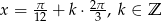Zadanie nr 4151424
Rozwiąż równanie 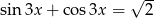 .
.
Rozwiązanie
Sposób I
Będziemy chcieli skorzystać ze wzoru na sinus sumy
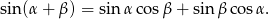
W tym celu przekształćmy podane równanie
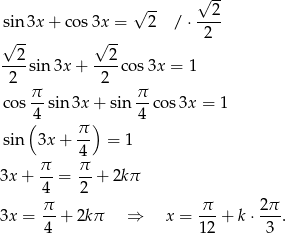
Sposób II
Skorzystamy ze wzorów
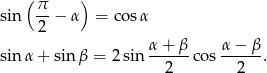
Przekształcamy równanie
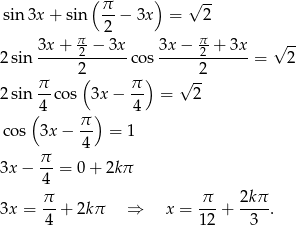
Odpowiedź: 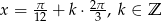
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 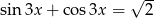 .
.
Sposób I
Będziemy chcieli skorzystać ze wzoru na sinus sumy
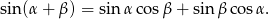
W tym celu przekształćmy podane równanie
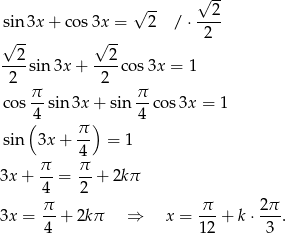
Sposób II
Skorzystamy ze wzorów
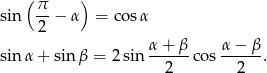
Przekształcamy równanie
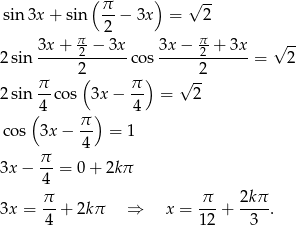
Odpowiedź: