/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 4986558

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 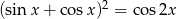2 (sin x + cos x) = cos 2x .

Rozwiązanie

Przekształcamy podane równanie

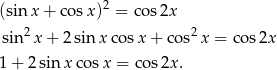
2 (sinx + co sx) = co s2x sin2 x+ 2sin xco sx + cos2x = cos 2x 1 + 2sin xco sx = c os2x .

W tym miejscu mamy co najmniej dwie możliwości.

Sposób I

Korzystamy ze wzoru na 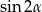sin 2α .

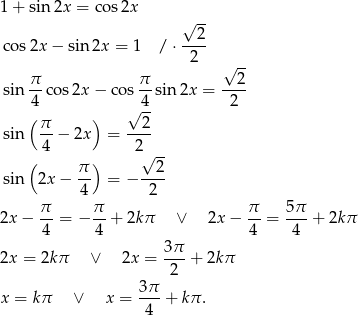
1+ sin 2x = co s2x √ -- --2- cos 2x− sin 2x = 1 / ⋅ 2 √ -- sin π-cos2x − cos π sin 2x = --2- 4 √ 4- 2 ( π ) 2 sin --− 2x = ---- ( 4 ) 2√ -- π- --2- sin 2x − 4 = − 2 π π π 5π 2x− -- = − -- + 2kπ ∨ 2x − -- = ---+ 2k π 4 4 4 4 2x = 2kπ ∨ 2x = 3π-+ 2kπ 2 3π- x = kπ ∨ x = 4 + kπ .

Sposób II

Tym razem postaramy sie zlikwidować 1 z lewej strony.

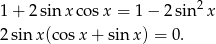
1 + 2 sin x cosx = 1− 2sin2x 2 sin x(co sx + sinx ) = 0.

Równość 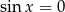sin x = 0 daje nam rozwiązania 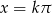x = kπ . Dalej zajmujemy się tylko wyrażeniem w nawiasie. Można tę równość rozwiązać na wiele sposobów, więc należy poniższy rachunek traktować wyłącznie jako jeden z przykładów.

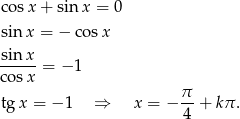
cosx + sin x = 0 sin x = − cos x sin-x- cosx = − 1 π tgx = − 1 ⇒ x = − -4 + kπ .

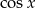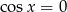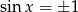Po drodze dzieliliśmy przez cos x , ale dla cos x = 0 mamy sin x = ± 1 i jest jasne, że równość nie zachodzi.  
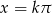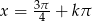Odpowiedź: x = kπ lub 3π- x = 4 + kπ , k ∈ C

Wersja PDF