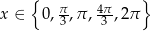/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 5491468

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 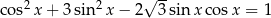2 2 √ -- cos x+ 3sin x− 2 3sin xco sx = 1 w przedziale ⟨0,2π ⟩ .

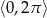Rozwiązanie

Sposób I

Przekształcamy dane równanie korzystając z jedynki trygonometrycznej.

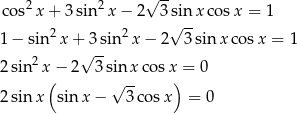
2 2 √ -- cos x + 3 sin x − 2 3 s√inx cos x = 1 1 − sin2 x+ 3sin2 x− 2 3sin xco sx = 1 √ -- 2 sin2x − 2 3 sinx cos x = 0 ( √ -- ) 2 sinx sin x− 3co sx = 0

Stąd 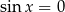sin x = 0 , czyli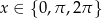 x ∈ {0,π ,2π }

PIC

lub

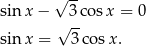
√ -- sinx − √ 3cos x = 0 sinx = 3co sx.

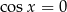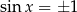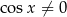Zauważmy, że jeżeli co sx = 0 , to powyższe równanie jest sprzeczne (bo wtedy sin x = ± 1 ), więc możemy założyć, że co sx ⁄= 0 .

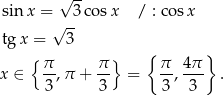
√ -- sin x = √ -3cos x / : cosx tgx = 3 { } { } x ∈ π-,π + π- = π-, 4π . 3 3 3 3

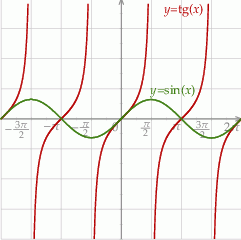
Dane równanie ma więc w przedziale 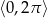⟨0 ,2π⟩ 5 rozwiązań

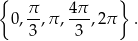
{ } π- 4π- 0, 3,π , 3 ,2π .

Sposób II

Przekształcamy dane równanie korzystając ze wzoru skróconego mnożenia na kwadrat różnicy.

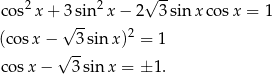
2 2 √ -- co s x + 3√ sin x − 2 3 sin x cosx = 1 (cos x− 3sin x)2 = 1 √ -- co sx − 3 sin x = ± 1 .

Teraz będziemy chcieli skorzystać ze wzoru sinus różnicy.

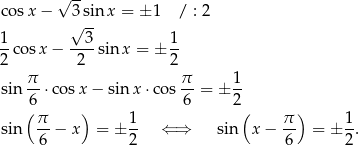
√ -- co sx − 3 sin x = ±1 / : 2 √ -- 1-cos x− --3-sin x = ± 1- 2 2 2 π- π- 1- sin 6 ⋅ cosx − sin x⋅co s 6 = ± 2 (π ) 1 ( π ) 1 sin -- − x = ± -- ⇐ ⇒ sin x − -- = ± -. 6 2 6 2

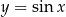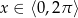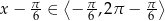W ostatniej równoważności skorzystaliśmy z tego, że funkcja y = sinx jest nieparzysta. W tym miejscu łatwo o pomyłkę, bo wprawdzie x ∈ ⟨0,2 π⟩ , ale ⟨ ⟩ x − π6-∈ − π6-,2π − π6 . Mamy zatem

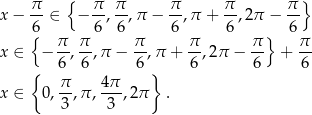
{ } x − π-∈ − π-, π-,π − π-,π + π-,2π − π- 6{ 6 6 6 6 } 6 x ∈ − π-, π-,π − π-,π + π-,2π − π- + π- { 6 6 6 } 6 6 6 π 4 π x ∈ 0 ,--,π,---,2 π . 3 3

 
Odpowiedź: { π 4π } x ∈ 0,-3,π, 3-,2π

Wersja PDF