/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 6228314

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 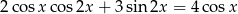2co sx cos2x + 3 sin2x = 4co sx .

Rozwiązanie

Korzystamy ze wzorów

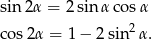
sin 2α = 2sin αcos α cos2 α = 1 − 2sin2 α.

Liczymy

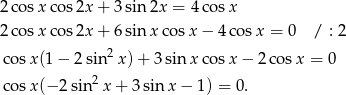
2 cosx cos 2x + 3sin 2x = 4 cos x 2 cosx cos 2x + 6sin xco sx − 4 cosx = 0 / : 2 cosx (1− 2sin2x )+ 3 sinx cosx − 2cos x = 0 2 cosx (−2 sin x + 3 sinx − 1) = 0.

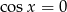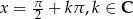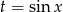Warunek cos x = 0 daje rozwiązania x = π2-+ k π,k ∈ C . Aby sprawdzić, kiedy zerem jest wyrażenie w drugim nawiasie podstawmy t = sin x .

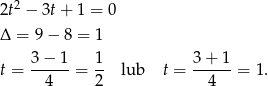
2t2 − 3t + 1 = 0 Δ = 9 − 8 = 1 3−--1- 1- 3-+-1- t = 4 = 2 lub t = 4 = 1.

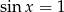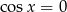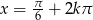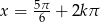Drugie rozwiązanie, czyli sin x = 1 nie daje nic nowego (bo wtedy cosx = 0 ), a pierwsze daje x = π-+ 2kπ 6 lub x = 5π-+ 2k π 6 .  
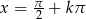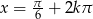Odpowiedź: x = π-+ kπ 2 lub x = π-+ 2k π 6 lub 5π x = 6--+ 2kπ , k ∈ C

Wersja PDF