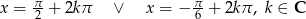Zadanie nr 6394242
Dana jest funkcja 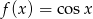 . Rozwiąż równanie
. Rozwiąż równanie 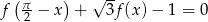 .
.
Rozwiązanie
Liczymy.
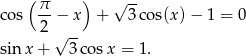
Teraz będziemy chcieli skorzystać ze wzoru na cosinus różnicy. Aby to zrobić dzielimy obie strony równania przez 2.
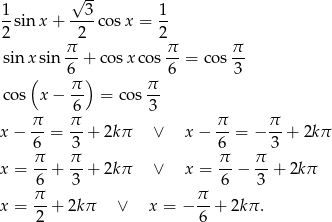
Odpowiedź: 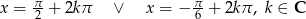
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dana jest funkcja 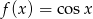 . Rozwiąż równanie
. Rozwiąż równanie 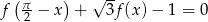 .
.
Liczymy.
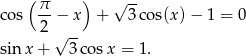
Teraz będziemy chcieli skorzystać ze wzoru na cosinus różnicy. Aby to zrobić dzielimy obie strony równania przez 2.
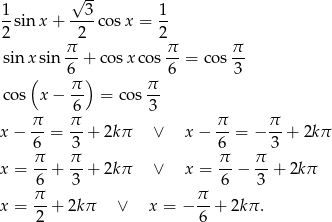
Odpowiedź: