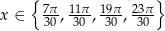Zadanie nr 6755945

Rozwiąż równanie 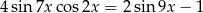4sin 7xco s2x = 2sin9x − 1 w przedziale ⟨0,π ⟩ .

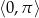Rozwiązanie

Sposób I

Skorzystamy ze wzorów na sinus sumy i różnicy

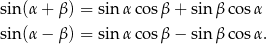
sin (α+ β) = sinα cos β+ sin β cos α sin (α− β) = sinα cos β− sin β cos α.

Przekształcamy równanie.

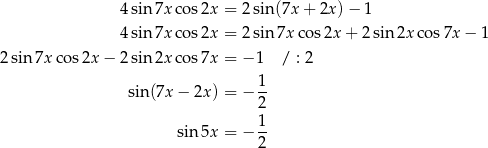
4sin 7xco s2x = 2sin(7x + 2x )− 1 4sin 7xco s2x = 2sin7x co s2x + 2 sin 2x cos7x − 1 2 sin 7x cos 2x− 2sin 2xco s7x = −1 / : 2 1 sin(7x − 2x) = − -- 2 sin 5x = − 1- 2

Szkicujemy teraz wykres sinusa.

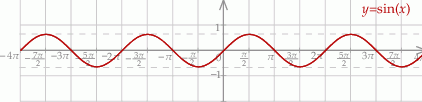
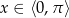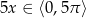Z wykresu odczytujemy rozwiązania – musimy odrobinę uważać, bo wprawdzie x ∈ ⟨0,π⟩ , ale 5x ∈ ⟨0,5 π⟩ .

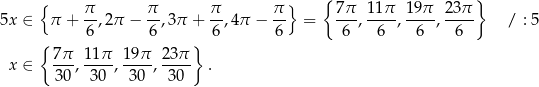
{ } { π- π- π- π-} 7π- 11-π 19π- 23π- 5x ∈ π + 6,2π − 6 ,3π + 6 ,4π − 6 = 6 , 6 , 6 , 6 / : 5 { } x ∈ 7π-, 11-π , 19π-, 23π . 3 0 30 30 30

Sposób II

Tym razem skorzystamy ze wzoru na sumę sinusów

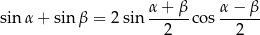
α-+-β- α-−-β- sinα + sin β = 2 sin 2 co s 2

Aby móc zastosować ten wzór szukamy i tak, aby

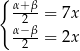
{ α+2-β= 7x α−-β 2 = 2x

Dodajemy i odejmujemy równania stronami i mamy 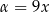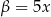α = 9x , β = 5x . Równanie możemy więc zapisać w postaci

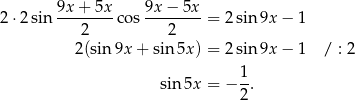
9x + 5x 9x − 5x 2⋅2 sin -------- cos-------- = 2 sin9x − 1 2 2 2(sin9x + sin 5x) = 2 sin9x − 1 / : 2 1 sin 5x = − -. 2

Rozwiązania odczytujemy tak samo jak w poprzednim sposobie.
Odpowiedź: { } x ∈ 73π0-, 131π0-, 193π0 , 233π0