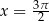/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 6757421

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 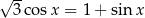√ -- 3co sx = 1 + sin x w przedziale ⟨0,2 π⟩ .

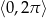Rozwiązanie

Sposób I

Przekształcimy równanie tak, aby móc skorzystać ze wzoru na cosinus sumy

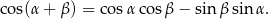
co s(α+ β) = cos αco sβ − sin βsin α.

Przekształcamy

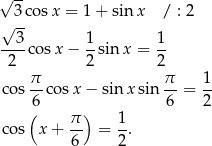
√ -- 3 cosx = 1+ sin x / : 2 √ -- ---3co sx − 1-sinx = 1- 2 2 2 π- π- 1- cos 6 cosx − sin xsin 6 = 2 ( π ) 1 cos x+ -- = -. 6 2

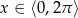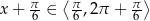Teraz trzeba odrobinę uważać, bo wprawdzie x ∈ ⟨0,2π⟩ , ale π- ⟨π- π-⟩ x + 6 ∈ 6 ,2π + 6 . Szkicujemy cosinusa.

PIC

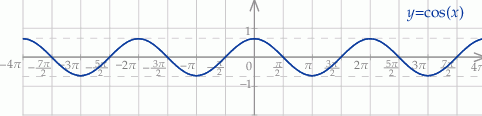
Odczytujemy rozwiązania.

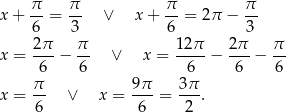
x + π- = π- ∨ x+ π- = 2π − π- 6 3 6 3 2π π 12π 2π π x = -6-− 6- ∨ x = -6--− -6-− 6- x = π- ∨ x = 9π-= 3π-. 6 6 2

Sposób II

Podnosimy równanie stronami do kwadratu – oczywiście możemy w ten sposób zwiększyć liczbę rozwiązań, więc na koniec będziemy musieli sprawdzić poprawność otrzymanych rozwiązań.

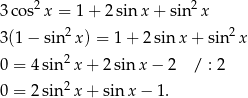
3co s2x = 1 + 2 sin x + sin2 x 2 2 3(1 − sin x) = 1+ 2sinx + sin x 0 = 4 sin 2x + 2 sin x − 2 / : 2 2 0 = 2 sin x + sinx − 1 .

Podstawiamy 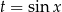t = sin x i mamy

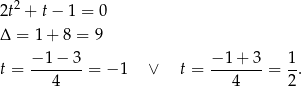
2t2 + t− 1 = 0 Δ = 1 + 8 = 9 t = −-1-−-3 = − 1 ∨ t = −-1-+-3 = 1. 4 4 2

Zatem

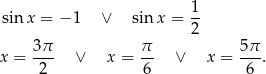
1 sinx = − 1 ∨ sinx = -- 2 x = 3π- ∨ x = π- ∨ x = 5π-. 2 6 6

To jednak nie koniec, bo musimy teraz sprawdzić otrzymane rozwiązania. Łatwo sprawdzić, że dwa pierwsze rozwiązania są OK, ale dla 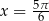x = 56π- lewa strona równania jest ujemna, a prawa dodatnia.  
Odpowiedź: 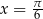π- x = 6 lub 3π- x = 2

Wersja PDF