/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 7127659

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 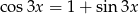cos 3x = 1 + sin 3x .

Rozwiązanie

Sposób I

Będziemy chcieli skorzystać ze wzoru

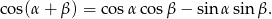
co s(α+ β) = cos αco sβ − sin αsin β.

W tym celu mnożymy obie strony równania przez π π √ 2 sin 4-= cos 4-= -2-

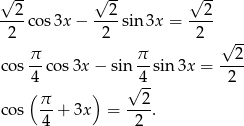
√ -- √ -- √ -- --2-cos 3x − --2-sin3x = --2- 2 2 2 -- π π √ 2 co s-- cos3x − sin --sin 3x = ---- 4 √4-- 2 ( π- ) --2- co s 4 + 3x = 2 .

I dalej już łatwo,

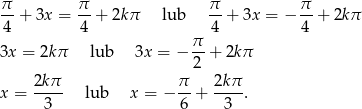
π- + 3x = π-+ 2kπ lub π-+ 3x = − π-+ 2kπ 4 4 4 4 π- 3x = 2kπ lub 3x = − 2 + 2kπ 2kπ π 2k π x = ---- lub x = − --+ ---- . 3 6 3

Sposób II

Chcemy skorzystać ze wzoru

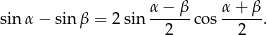
sin α − sinβ = 2 sin α-−-β-cos α-+-β-. 2 2

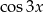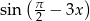W tym celu zamienimy co s3x na (π ) sin 2-− 3x .

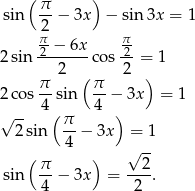
( π ) sin --− 3x − sin 3x = 1 2π- π- 2sin 2-−-6x-cos 2- = 1 2 2 π- (π- ) 2cos 4 sin 4 − 3x = 1 √ -- ( π ) 2sin --− 3x = 1 ( 4 ) √ -- sin π-− 3x = --2. 4 2

Ponieważ

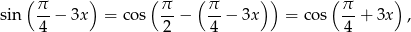
( π ) ( π (π ) ) ( π ) sin --− 3x = cos --− -- − 3x = co s --+ 3x , 4 2 4 4

otrzymane równanie jest identyczne z tym otrzymanym w sposobie I.  
Odpowiedź: x = 2kπ3- lub x = − π6 + 2k3π , k ∈ Z

Wersja PDF