Zadanie nr 7350807
Rozwiąż równanie 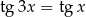 .
.
Rozwiązanie
Będziemy korzystać z warunku (który łatwo odczytać z wykresu)
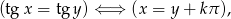
gdzie 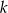 jest liczbą całkowitą.
jest liczbą całkowitą.
Liczymy
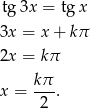
To jeszcze nie koniec, bo jak dotąd nie zajęliśmy się dziedziną równania.
Jeżeli 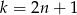 jest liczbą nieparzystą to
jest liczbą nieparzystą to 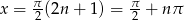 i liczby te nie należą do dziedziny tangensa.
i liczby te nie należą do dziedziny tangensa.
Jeżeli natomiast 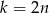 jest liczbą parzystą to
jest liczbą parzystą to 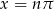 i wszystko jest OK (obie strony równania są równe 0).
i wszystko jest OK (obie strony równania są równe 0).
Odpowiedź: