/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 7407024

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 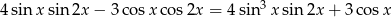3 4sin xsin 2x− 3co sx cos2x = 4sin xsin 2x+ 3co sx w przedziale ⟨0 ,2π⟩ .

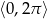Rozwiązanie

Korzystamy ze wzorów

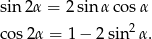
sin 2α = 2sin αcos α cos2 α = 1 − 2sin2 α.

Sposób I

Przekształcamy równanie

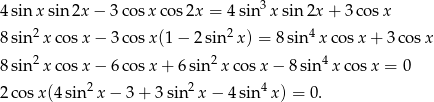
3 4 sinx sin 2x − 3 cos xcos 2x = 4 sin x sin 2x + 3 cos x 8 sin2x cosx − 3 cos x(1− 2sin2 x) = 8 sin 4x cosx + 3 cosx 8 sin2x cosx − 6 cos x+ 6sin2 xcos x− 8sin4 xco sx = 0 2 2 4 2 cosx (4sin x− 3+ 3sin x − 4 sin x ) = 0.

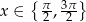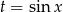Otrzymujemy stąd rozwiązanie x ∈ { π-, 3π} 2 2 . Aby rozwiązać równanie w nawiasie podstawiamy t = sin x .

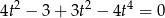
2 2 4 4t − 3 + 3t − 4t = 0

Powyższe równanie możemy rozwiązać szukając pierwiastków całkowitych, ale zamiast tego można łatwo zauważyć, że możemy wyłączyć 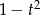2 1− t .

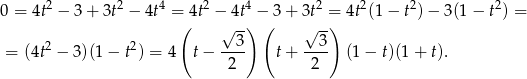
0 = 4t2 − 3 + 3t2 − 4t4 = 4t2 − 4t4 − 3 + 3t2 = 4t2(1 − t2)− 3(1− t2) = ( √ -) ( √ --) = (4t2 − 3)(1 − t2) = 4 t− --3- t+ --3- (1 − t)(1+ t). 2 2

Zauważmy, że rozwiązania 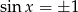sin x = ± 1 nie wnoszą nic nowego, bo wtedy 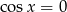cosx = 0 . Pozostaje zatem warunek 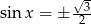√- sin x = ± -3- 2 , który w danym przedziale spełniają liczby

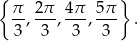
{ π 2 π 4π 5π } --,---, ---,--- . 3 3 3 3

Sposób II

Tym razem skorzystamy ze wzoru

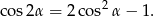
2 co s2α = 2cos α− 1.

Przekształcamy równanie

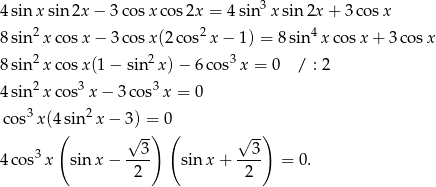
3 4 sin x sin 2x − 3 cosx cos 2x = 4 sin x sin 2x + 3 cosx 8 sin 2x cosx − 3 cosx (2co s2 x − 1) = 8 sin 4x cosx + 3 cosx 2 2 3 8 sin x cosx (1− sin x)− 6co s x = 0 / : 2 4 sin 2x cos3x − 3 cos3x = 0 cos3x(4 sin2x − 3) = 0 ( √ --) ( √ -) 4 cos3x sin x − --3- sinx + --3- = 0. 2 2

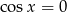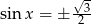Zatem co sx = 0 lub √ - sin x = ± -23 . Mamy stąd

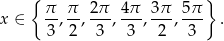
{ } x ∈ π-, π-, 2π-, 4π-, 3π-, 5π . 3 2 3 3 2 3

 
Odpowiedź: { } π-, π-, 2π, 4π-, 3π, 5π 3 2 3 3 2 3

Wersja PDF