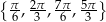/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 8391527

Rozwiąż równanie 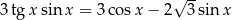√ -- 3tg xsin x = 3 cosx − 2 3 sinx w przedziale ⟨0,2π ⟩ .

Wersja PDF

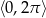Rozwiązanie

Ze względu na tangens musi być 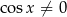cosx ⁄= 0 .

Sposób I

Przekształcamy dane równanie – łatwo zauważyć, że jak podzielimy równanie przez 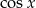cosx , to otrzymamy równanie z samymi tangensami.

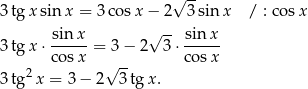
√ -- 3tg xsin x = 3 cosx − 2 3sinx / : co sx sinx- √ -- sin-x 3tg x⋅ cosx = 3 − 2 3 ⋅cos x 2 √ -- 3tg x = 3 − 2 3 tg x.

Podstawiamy teraz 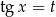tg x = t .

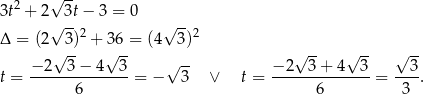
2 √ -- 3t + 2 √ 3t− 3 = 0 √ -- Δ = (2 3)2 + 36 = (4 3)2 √ -- √ -- √ -- √ -- √ -- −-2--3-−-4--3- √ -- −-2--3-+-4--3- --3- t = 6 = − 3 ∨ t = 6 = 3 .

Mamy zatem

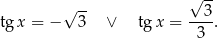
√ -- √ -- 3 tgx = − 3 ∨ tgx = -3-.

Szkicujemy tangensa.

PIC

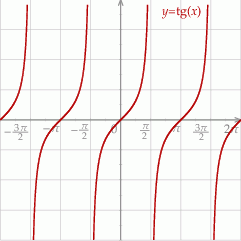
Odczytujemy z wykresu rozwiązanie.

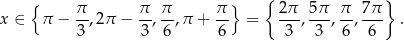
{ } { π π π π } 2π 5π π 7π x ∈ π − 3,2 π − -3,-6,π + 6- = 3--,-3-,6-,-6- .

Sposób II

Pozbywamy się tangensa podstawiając 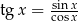sinx tg x = cosx .

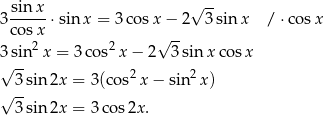
sin x √ -- 3----- ⋅sin x = 3cos x− 2 3sin x / ⋅co sx cos2x 2 √ -- 3sin x = 3co s x − 2 3 sin x cosx √ -- 2 2 √ 3sin 2x = 3(co s x − sin x) 3sin 2x = 3 cos2x .

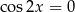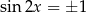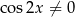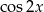Zauważmy teraz, że jeżeli cos 2x = 0 to sin2x = ± 1 i powyższe równanie jest sprzeczne. Zatem cos2x ⁄= 0 i możemy podzielić powyższe równanie przez cos2x .

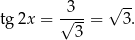
√ -- tg 2x = √3--= 3. 3

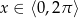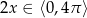Teraz trzeba odrobinę uważać, bo w prawdzie x ∈ ⟨0,2 π⟩ , ale 2x ∈ ⟨0,4π ⟩ . Mamy zatem

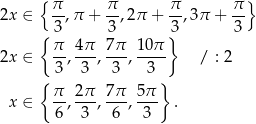
{ } 2x ∈ π-,π + π-,2π + π,3 π + π- { 3 3 }3 3 π 4π 7π 10π 2x ∈ 3, 3--,-3-,-3-- / : 2 { } π- 2π- 7π- 5π- x ∈ 6, 3 , 6 , 3 .

 
Odpowiedź: { π- 2π-7π- 5π} 6 ,3 , 6 ,3

Wersja PDF