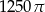/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 8720736

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz sumę wszystkich miejsc zerowych funkcji 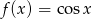f(x ) = cosx należących do przedziału ⟨0;50π ⟩ .

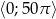Rozwiązanie

Miejsca zerowe cosinusa są postaci 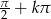π- 2 + kπ . W podanym przedziale są zatem

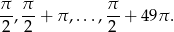
π π π --,-- + π ,...,--+ 4 9π. 2 2 2

Są to kolejne wyrazy ciągu arytmetycznego o pierwszym wyrazie 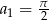a = π- 1 2 i różnicy 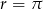r = π . Jego suma jest więc równa

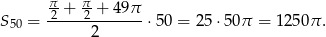
π-+ π-+ 49π S50 = -2---2------- ⋅50 = 2 5⋅50 π = 1 250π . 2

 
Odpowiedź: 125 0π

Wersja PDF