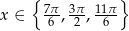Zadanie nr 8922066
Rozwiąż równanie 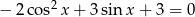 w przedziale
w przedziale 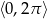 .
.
Rozwiązanie
Korzystając z jedynki trygonometrycznej możemy równanie zapisać w postaci
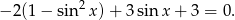
Po podstawieniu 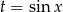 mamy
mamy
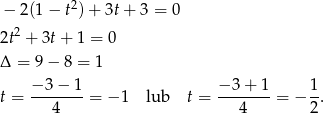
Mamy zatem
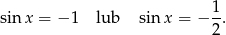
Szkicujemy sinusa.
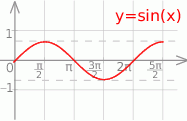
Z wykresu odczytujemy rozwiązania.
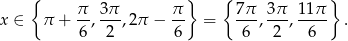
Odpowiedź: 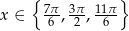
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 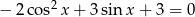 w przedziale
w przedziale 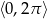 .
.
Korzystając z jedynki trygonometrycznej możemy równanie zapisać w postaci
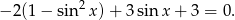
Po podstawieniu 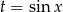 mamy
mamy
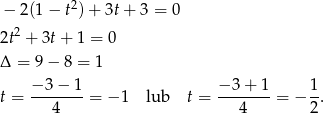
Mamy zatem
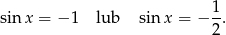
Szkicujemy sinusa.

Z wykresu odczytujemy rozwiązania.
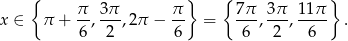
Odpowiedź: