Zadanie nr 8959252

Wyznaczyć wartości 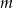dla których równanie

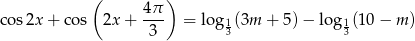
( 4π ) cos2x + co s 2x + --- = log1(3m + 5) − log 1(10− m) 3 3 3

ma rozwiązania.

Rozwiązanie

Sprawdźmy najpierw kiedy prawa strona ma sens.

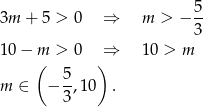
5 3m + 5 > 0 ⇒ m > − -- 3 10 − m > 0 ⇒ 1 0 > m ( 5 ) m ∈ − -,10 . 3

Przekształćmy podane równanie

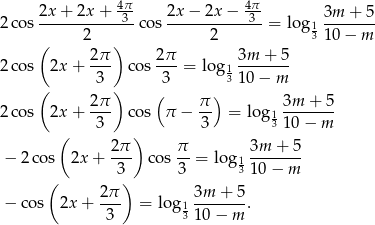
4π- 4π- 2 cos 2x-+-2x-+--3-co s 2x-−-2x-−-3- = log 13m--+-5 2 2 31 0− m ( 2π ) 2π 3m + 5 2 cos 2x + --- cos ---= lo g1 ------- ( 3 ) 3 3 10 − m 2π- ( π-) 3m-+--5 2 cos 2x + 3 cos π − 3 = log13 10 − m ( ) − 2 cos 2x + 2-π cos π = log 13m--+-5 3 3 31 0− m ( 2π ) 3m + 5 − cos 2x + --- = log1 -------. 3 3 10 − m

Równanie to będzie miało rozwiązanie o ile prawa strona będzie w przedziale 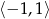⟨− 1,1⟩ .

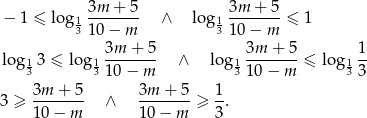
3m + 5 3m + 5 − 1 ≤ log1 ------- ∧ log 1------- ≤ 1 3 10 − m 310 − m log 13 ≤ log 13m--+-5 ∧ log 13m--+-5 ≤ lo g1 1- 3 310 − m 31 0− m 3 3 3m + 5 3m + 5 1 3 ≥ ------- ∧ ------- ≥ --. 10 − m 10− m 3

Z założenia 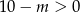10 − m > 0 , więc możemy pomnożyć przez mianownik.

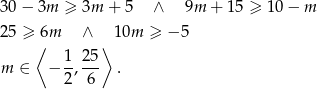
30 − 3m ≥ 3m + 5 ∧ 9m + 15 ≥ 10− m 25 ≥ ⟨6m ∧ ⟩ 10m ≥ − 5 1 25 m ∈ − -, --- . 2 6

Odpowiedź: ⟨ 1 25⟩ m ∈ − 2 ,6-