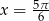Zadanie nr 9185615
Rozwiąż równanie 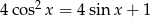 w przedziale
w przedziale 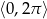 .
.
Rozwiązanie
Korzystając z jedynki trygonometrycznej możemy równanie zapisać w postaci
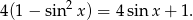
Po podstawieniu 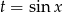 mamy
mamy
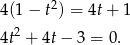
Dalej, 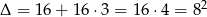 ,
, 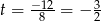 lub
lub 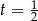 . Pierwszy z pierwiastków odrzucamy, bo
. Pierwszy z pierwiastków odrzucamy, bo 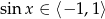 . Zatem
. Zatem 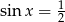 czyli
czyli 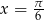 lub
lub 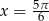 .
.
Odpowiedź: 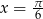 lub
lub