Zadanie nr 9195132
Dana jest funkcja 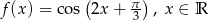 .
.
- Narysuj wykres funkcji
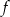 dla
dla 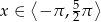 .
. - Rozwiąż równanie:
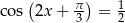 , dla
, dla 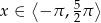 .
.
Rozwiązanie
- Zapiszmy wzór funkcji
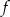 w postaci
w postaci 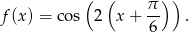
Teraz widać, że wykres funkcji
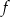 powstaje z wykresu funkcji
powstaje z wykresu funkcji 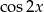 przez przesunięcie o
przez przesunięcie o 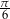 w lewo. Wykres funkcji
w lewo. Wykres funkcji 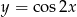 wygląda natomiast jak zwykły cosinus, ale z dziedziną ściśniętą dwa razy (wartość w punkcie
wygląda natomiast jak zwykły cosinus, ale z dziedziną ściśniętą dwa razy (wartość w punkcie  jest taka sama jak wartość w punkcie
jest taka sama jak wartość w punkcie 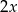 zwykłego cosinusa). Możemy teraz naszkicować wykres (trzeba jeszcze pamiętać o obcięciu wykresu do podanego przedziału).
zwykłego cosinusa). Możemy teraz naszkicować wykres (trzeba jeszcze pamiętać o obcięciu wykresu do podanego przedziału). 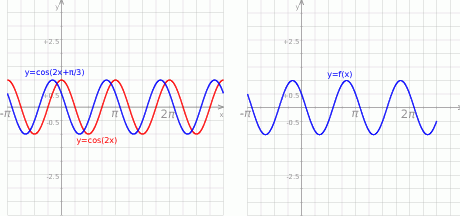
- Liczymy
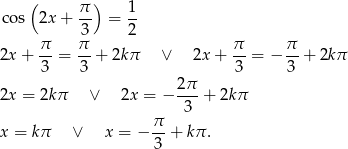
Z wykresu widać, że w podanym przedziale będą następujące rozwiązania
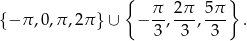
Odpowiedź: