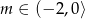/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 9364693

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 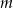m , dla których równanie 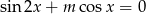sin 2x + m co sx = 0 ma w przedziale 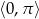⟨0,π⟩ trzy rozwiązania.

Rozwiązanie

Na mocy wzoru na 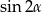sin 2α dane równanie możemy zapisać w postaci

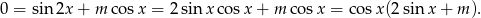
0 = sin 2x + m cos x = 2 sin x cosx + m cosx = cosx (2sinx + m ).

Widać teraz, że jednym z pierwiastków jest 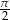π- 2 . Pytanie teraz brzmi kiedy równanie

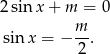
2 sinx + m = 0 m sin x = − --. 2

ma dwa rozwiązania w przedziale 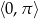⟨0,π ⟩ , które są różne od 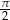π- 2 . Szkicujemy sinusa

PIC

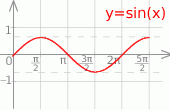
Z wykresu widać, że powyższe równanie z sinusem ma dwa rozwiązania gdy 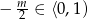− m2-∈ ⟨0,1 ) , tzn. gdy

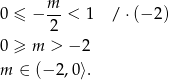
0 ≤ − m-< 1 / ⋅ (−2 ) 2 0 ≥ m > − 2 m ∈ (− 2,0⟩.

 
Odpowiedź: m ∈ (− 2,0⟩

Wersja PDF