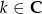/Szkoła średnia/Równania/Trygonometryczne

Zadanie nr 9545444

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 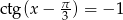π- ctg(x − 3) = − 1 .

Rozwiązanie

Zacznijmy od wykresu cotangensa.

PIC

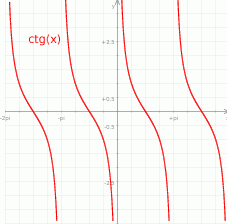
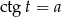Z wykresu widać, że jeżeli mamy jakiekolwiek rozwiązanie α równania ctg t = a to wszystkie rozwiązania są postaci

t = α + kπ ,

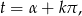
gdzie 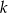k dowolna liczba całkowita.

Rozwiązaniem równania 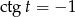ctgt = − 1 są liczby postaci:

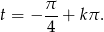
t = − π-+ kπ. 4

U nas 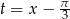t = x − π3 , zatem

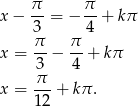
π π x − --= − --+ kπ 3 4 x = π- − π-+ kπ 3 4 x = π--+ k π. 12

 
Odpowiedź: 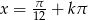x = π-+ kπ 12 , gdzie k ∈ C

Wersja PDF