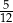/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Nierówności

Zadanie nr 1108092

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru sześciu liczb 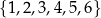{1,2,3 ,4,5,6} losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 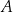A polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.

Rozwiązanie

Parę liczb możemy wylosować na

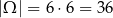
|Ω | = 6⋅6 = 36

sposobów (uwzględniamy kolejność losowania).

Sposób I

Zdarzenia sprzyjające 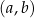(a ,b) to takie, że a > b :

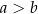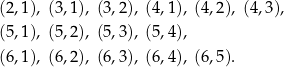
(2,1), (3,1), (3,2), (4 ,1), (4,2), (4,3), (5,1), (5,2), (5,3), (5 ,4), (6,1), (6,2), (6,3), (6 ,4), (6,5).

Jest więc 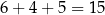6 + 4 + 5 = 15 zdarzeń sprzyjających i interesujące nas prawdopodobieństwo jest równe

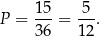
P = 15-= 5-. 36 12

Sposób II

Wśród 36 par postaci 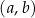(a,b) jest 6 takich, w których a = b :

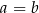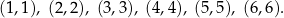
(1,1), (2,2), (3,3), (4 ,4), (5,5), (6,6).

Wśród pozostałych 30 par jest dokładnie tyle samo par spełniających nierówność 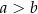a > b , co par spełniających nierówność przeciwną 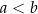a < b (bo z każdej pary pierwszego typu możemy zrobić dokładnie jedną parę drugiego typu i odwrotnie). Jest więc 15 par spełniających nierówność 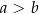a > b i interesujące nas prawdopodobieństwo jest równe

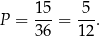
P = 15-= 5-. 36 12

 
Odpowiedź: 152

Wersja PDF