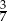Zadanie nr 2197729
Ze zbioru 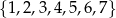 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 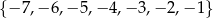 liczbę
liczbę 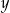 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 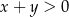 .
.
Rozwiązanie
Wszystkich zdarzeń elementarnych jest
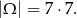
Jeżeli wylosujemy 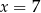 , to
, to 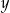 może przyjąć jedną z wartości:
może przyjąć jedną z wartości: 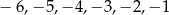 .
.
Jeżeli wylosujemy 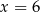 , to
, to 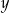 może przyjąć jedną z wartości:
może przyjąć jedną z wartości: 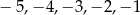 .
.
Jeżeli wylosujemy 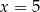 , to
, to 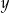 może przyjąć jedną z wartości:
może przyjąć jedną z wartości: 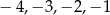 .
.
Jeżeli wylosujemy 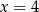 , to
, to 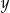 może przyjąć jedną z wartości:
może przyjąć jedną z wartości: 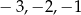 .
.
Jeżeli wylosujemy 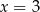 , to
, to 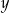 może przyjąć jedną z wartości:
może przyjąć jedną z wartości: 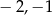 .
.
Jeżeli wylosujemy 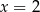 , to musi być
, to musi być 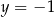 . Jest zatem
. Jest zatem
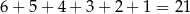
zdarzeń sprzyjających i prawdopodobieństwo wynosi
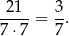
Odpowiedź: