/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Nierówności

Zadanie nr 4486754

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru liczb 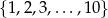{1,2,3,...,1 0} losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.

Rozwiązanie

Parę liczb możemy wylosować na

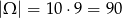
|Ω | = 10 ⋅9 = 90

sposobów (kolejność jest ważna, bo od niej zależy wynik odejmowania).

Zdarzenia sprzyjające 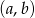(a,b) to takie, że 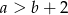a > b + 2 . Wypiszmy je w zależności od tego ile jest równe b .

(4,1 ),(5 ,1),(6,1),(7,1),(8,1),(9,1),(10 ,1 ) (5,2 ),(6 ,2),(7,2),(8,2),(9,2),(10,2) (6,3 ),(7 ,3),(8,3),(9,3),(10,3) (7,4 ),(8 ,4),(9,4),(10,4) (8,5 ),(9 ,5),(10,5) (9,6 ),(1 0,6) (10 ,7).

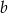W sumie jest tych zdarzeń

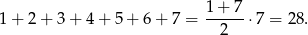
1+ 2+ 3+ 4+ 5+ 6+ 7 = 1-+-7-⋅7 = 28 . 2

Zatem prawdopodobieństwo wynosi

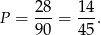
28 14 P = ---= --. 90 45

 
Odpowiedź: 1445

Wersja PDF