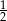/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Nierówności

Zadanie nr 4856195

Dany jest zbiór 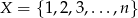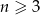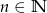X = {1,2,3 ,...,n } , n ≥ 3 , n ∈ N . Ze zbioru 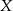X losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo, że pierwsza z wylosowanych liczb jest większa od drugiej.

Wersja PDF

Rozwiązanie

Sposób I

Jeżeli ustalimy, że zdarzenia elementarne to pary liczb 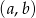(a ,b ) , gdzie 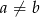a ⁄= b (losujemy bez zwracania!), to par w których 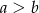a > b jest dokładnie tyle samo co par, w których 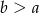b > a . Oznacza to, że szukane prawdopodobieństwo wynosi 12 .

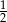Sposób II

Jeżeli ktoś woli rachunki, to policzmy. Przyjmujemy za zdarzenia elementarne pary 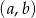(a ,b) wylosowanych liczb. Zatem

|Ω | = n(n − 1 )

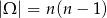
(pierwszą liczbę możemy wybrać na n sposobów, drugą na n − 1 ).

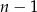Teraz liczmy zdarzenia sprzyjające, czyli pary 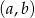(a,b) , gdzie 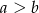a > b . Ile ich jest? Dokładnie

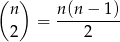
( ) n = n(n-−-1)- 2 2

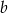(musimy wybrać dwie liczby a i b z podanego zbioru i zrobić z nich parę taką, żeby 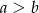a > b - nie ma tu żadnego wyboru). Zatem szukane prawdopodobieństwo jest równe

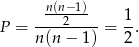
n(n−2-1) 1 P = --------- = -. n (n− 1) 2

 
Odpowiedź: 1 2

Wersja PDF