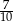/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Nierówności

Zadanie nr 4950658

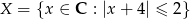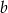Ze zbioru X = {x ∈ C : |x + 4| ≤ 2} losujemy dwa razy (bez zwracania) po jednej liczbie. Oznaczamy te liczby w kolejności losowania przez a oraz b . Oblicz prawdopodobieństwo tego, że wylosowana para liczb 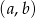(a,b) jest rozwiązaniem nierówności x − y − 2 < 0 .

Wersja PDF

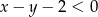Rozwiązanie

Zacznijmy od ustalenia czym jest zbiór 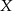X .

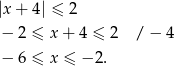
|x+ 4| ≤ 2 − 2 ≤ x + 4 ≤ 2 / − 4 − 6 ≤ x ≤ − 2.

Zatem

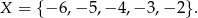
X = { − 6,− 5,− 4,− 3,− 2}.

W szczególności

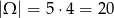
|Ω | = 5⋅4 = 20

(pierwszą liczbę możemy wybrać na 5 sposobów, a drugą na 4 sposoby).

Łatwo sprawdzić, że rozwiązaniem nierówności 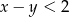x − y < 2 są pary

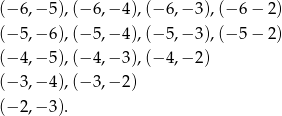
(−6 ,−5 ),(− 6 ,− 4 ),(− 6 ,− 3 ),(− 6 − 2) (−5 ,−6 ),(− 5 ,− 4 ),(− 5 ,− 3 ),(− 5 − 2) (−4 ,−5 ),(− 4 ,− 3 ),(− 4 ,− 2 ) (−3 ,−4 ),(− 3 ,− 2 ) (−2 ,−3 ).

Zatem prawdopodobieństwo wynosi

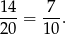
14-= -7-. 20 1 0

 
Odpowiedź: 170

Wersja PDF