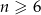/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Nierówności

Zadanie nr 5074950

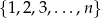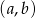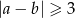Ze zbioru {1,2,3,...,n} losujemy bez zwracania parę liczb (a ,b) . Dla jakich n prawdopodobieństwo wylosowania pary spełniającej warunek |a− b| ≥ 3 jest większe od 13 ?

Wersja PDF

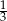Rozwiązanie

Parę liczb możemy wybrać na

|Ω | = n ⋅(n − 1)

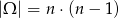
sposobów. Par spełniających podany warunek jest dość sporo, więc łatwiej będzie nam policzyć prawdopodobieństwo zdarzenia przeciwnego. Pytanie zatem brzmi: dla jakich n prawdopodobieństwo zdarzenia przeciwnego jest mniejsze od 2 3 ?

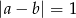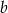Jeżeli |a − b| = 1 to liczby a i b są sąsiednie. Jest 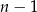n − 1 par liczb sąsiednich:

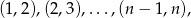
(1,2),(2,3),...,(n − 1,n ),

ale ponieważ uwzględniamy kolejność mamy 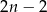2n − 2 takich par.

Jeżeli 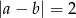|a − b| = 2 to mamy następujące możliwości:

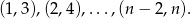
(1,3),(2,4),...,(n − 2,n ).

Pamiętając jeszcze o zmianie kolejności mamy 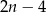2n − 4 takich par. Pozostało więc rozwiązać nierówność

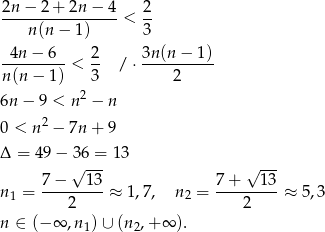
2n − 2 + 2n − 4 2 ----------------< -- n(n − 1) 3 -4n-−-6-- 2- 3n-(n−--1) n(n − 1 ) < 3 / ⋅ 2 2 6n − 9 < n − n 2 0 < n − 7n + 9 Δ = 49− 36 = 13 √ --- √ --- n1 = 7-−---1-3 ≈ 1,7, n2 = 7-+---13-≈ 5,3 2 2 n ∈ (− ∞ ,n1) ∪ (n2,+ ∞ ).

Ponieważ interesują na liczby naturalne n , mamy n ≥ 6 .  
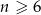Odpowiedź: n ≥ 6

Wersja PDF