/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Nierówności

Zadanie nr 8506183

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru liczb naturalnych spełniających nierówność 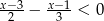x−-3- x−1- 2 − 3 < 0 losujemy dwie różne liczby 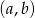(a,b) . Oblicz prawdopodobieństwo zdarzenia: punkt o współrzędnych 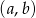(a,b ) należy do wykresu funkcji y = x + 4 .

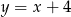Rozwiązanie

Wyznaczamy liczby spełniające nierówność

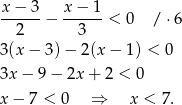
x− 3 x − 1 ------− ------< 0 / ⋅6 2 3 3(x− 3)− 2(x− 1) < 0 3x− 9− 2x+ 2 < 0 x− 7 < 0 ⇒ x < 7.

Jedynymi liczbami naturalnymi spełniającymi tą nierówność są

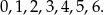
0,1,2,3,4,5,6 .

Ponieważ losujemy dwie różne liczby ze zbioru rozwiązań nierówności, więc możemy to zrobić na

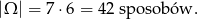
|Ω | = 7⋅ 6 = 42 sposob ów .

Zastanówmy się, jakie pary liczb należą do wykresu funkcji 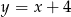y = x+ 4 . Widać, że

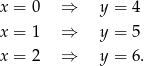
x = 0 ⇒ y = 4 x = 1 ⇒ y = 5 x = 2 ⇒ y = 6.

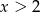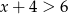Jeżeli natomiast x > 2 to x + 4 > 6 i wychodzimy poza zbiór rozwiązań nierówności.

Zatem prawdopodobieństwo jest równe

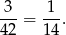
3 1 ---= ---. 42 1 4

 
Odpowiedź: -1 14

Wersja PDF