/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Nierówności

Zadanie nr 9559746

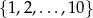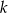Ze zbioru {1,2,...,10} losujemy dwie różne liczby n i k . Oblicz prawdopodobieństwo, że

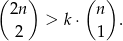
( ) ( ) 2n > k ⋅ n . 2 1
Wersja PDF

Rozwiązanie

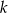Ponieważ liczby n i k pełnią inne role w danej nierówności, wygodniej będzie nam traktować zdarzenia elementarne jak pary uporządkowane 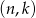(n,k) . Mamy więc

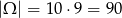
|Ω | = 10 ⋅9 = 90

(drugą liczbę możemy wybrać na 9 sposobów, bo liczby nie mogą być równe).

Spróbujmy teraz rozszyfrować podaną nierówność.

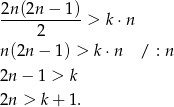
2n (2n − 1) ----------- > k⋅n 2 n(2n − 1) > k⋅ n / : n 2n − 1 > k 2n > k+ 1.

Zauważmy, że 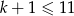k + 1 ≤ 11 , więc jeżeli 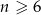n ≥ 6 to nierówność będzie spełniona dla wszystkich wartości 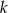k . Jest

5 ⋅9 = 45

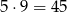
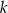takich zdarzeń (jest 5 możliwości wybrania n i 9 możliwości wybrania k różnego od n ).

Wypiszmy teraz możliwe wartości 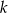k dla mniejszych wartości n .

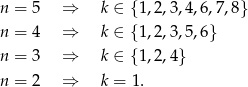
n = 5 ⇒ k ∈ {1,2,3,4,6 ,7 ,8} n = 4 ⇒ k ∈ {1,2,3,5,6 } n = 3 ⇒ k ∈ {1,2,4} n = 2 ⇒ k = 1.

Daje to nam

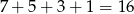
7+ 5+ 3+ 1 = 16

zdarzeń sprzyjających i prawdopodobieństwo jest równe

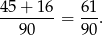
45-+-16-= 61-. 90 90

 
Odpowiedź: 6910

Wersja PDF