Zadanie nr 1177571
Ze zbioru wszystkich liczb trzycyfrowych losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 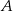 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
Rozwiązanie
Wszystkich liczb trzycyfrowych jest
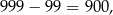
więc każdą z liczb możemy wylosować na 900 sposobów. Zatem jest
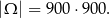
zdarzeń elementarnych.
W zdarzeniach sprzyjających obie wylosowane liczby muszą być nieparzyste, a wśród 900 liczb trzycyfrowych:
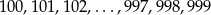
dokładnie połowa to liczby nieparzyste. Jest zatem
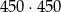
zdarzeń sprzyjających i interesujące nas prawdopodobieństwo jest równe
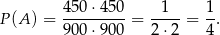
Odpowiedź: