/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość

Zadanie nr 1730086

Dodaj do ulubionych
Dodaj do rozwiązanych

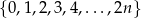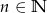Ze zbioru {0,1,2,3,4,...,2n } gdzie n ∈ N wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi 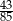4835 . Wyznacz ile liczb było w zbiorze.

Rozwiązanie

Zauważmy, że liczby nieparzyste w danym zbiorze to

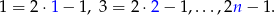
1 = 2 ⋅1 − 1, 3 = 2 ⋅2− 1,...,2n − 1.

Jest ich więc n . Podobnie, liczby parzyste to

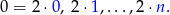
0 = 2⋅0 , 2 ⋅1,...,2 ⋅n.

Jest ich więc n + 1 .

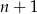Jeżeli za zdarzenia elementarne przyjmiemy nieuporządkowane trójki wylosowanych liczb, to

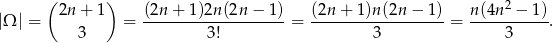
( ) 2n + 1 (2n-+-1)2n-(2n−--1)- (2n+--1)n(2n-−-1-)- n-(4n2 −-1) |Ω| = 3 = 3 ! = 3 = 3 .

Jeżeli suma wylosowanych liczb jest nieparzysta, to albo wszystkie są nieparzyste, albo dwie są parzyste i jedna jest nieparzysta. Mamy więc

( ) ( ) n n + 1 n(n-−-1)(n-−-2)- (n-+--1)n 3 + n ⋅ 2 = 3 ! + n ⋅ 2! = [ 2 2 ] 2 2 n--−--3n+--2 n--+-n- 4n--+--2 n-(2n--+-1) = n 6 + 2 = n ⋅ 6 = 3

zdarzeń sprzyjających (wybieramy trzy liczby nieparzyste lub jedną liczbę nieparzystą i dwie parzyste). Zatem

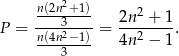
2 n(2n3+-1)- 2n-2 +-1 P = n(4n2−-1)-= 4n 2 − 1 . 3

Pozostało rozwiązań równanie

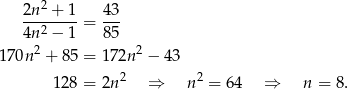
2 2n--+--1 = 43- 4n 2 − 1 85 170n 2 + 85 = 172n 2 − 43 1 28 = 2n 2 ⇒ n2 = 64 ⇒ n = 8.

W takim razie w danym zbiorze było 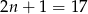2n + 1 = 1 7 liczb.  
Odpowiedź: 17

Wersja PDF