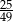/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość

Zadanie nr 1995979

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru liczb 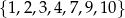{1,2,3,4 ,7 ,9,10} losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.

Rozwiązanie

Każdą liczbę możemy wybrać na 7 sposobów, więc

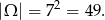
2 |Ω | = 7 = 4 9.

Policzmy teraz zdarzenia sprzyjające. Mamy dwie możliwości.

Obie liczby są nieparzyste. Takich zdarzeń jest

4 ⋅4 = 16

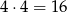
(bo każdą z liczb można wybrać na 4 sposoby).

Obie liczby są parzyste. Takich zdarzeń jest

3⋅ 3 = 9

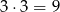
(bo każdą z liczb można wybrać na 3 sposoby).

Zatem prawdopodobieństwo jest równe

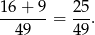
16+--9- 2-5 49 = 4 9.

 
Odpowiedź: 25 49

Wersja PDF