/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość

Zadanie nr 2954217

Spośród liczb 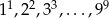1 2 3 9 1 ,2 ,3 ,...,9 wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.

Wersja PDF

Rozwiązanie

Za zdarzenia elementarne przyjmujemy nieuporządkowane trójki wylosowanych liczb. Zatem

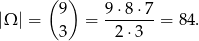
( ) |Ω | = 9 = 9⋅-8⋅7-= 84. 3 2 ⋅3

Sposób I

Najłatwiej jest policzyć prawdopodobieństwo zdarzenia przeciwnego, tzn. że iloczyn wylosowanych liczb jest nieparzysty. W podanym zbiorze jest 5 liczb nieparzystych, zatem mamy

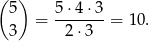
( ) 5 5⋅4-⋅3- 3 = 2⋅ 3 = 10.

trójek liczb nieparzystych. Zatem

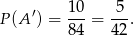
′ 10- -5- P(A ) = 84 = 42 .

Stąd

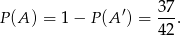
37 P(A ) = 1 − P(A ′) = ---. 42

Sposób II

Jeżeli ktoś nie chce liczyć zdarzenia przeciwnego, to można też liczyć wprost. Iloczyn będzie parzysty, gdy wszystkie trzy, dokładnie dwie lub dokładnie jedna liczba jest parzysta. Daje nam to

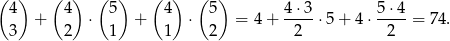
( 4) ( 4) (5) ( 4) ( 5) 4 ⋅3 5⋅ 4 + ⋅ + ⋅ = 4 + ---- ⋅5 + 4⋅ ---- = 74. 3 2 1 1 2 2 2

Zatem prawdopodobieństwo wynosi

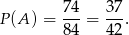
P (A) = 74-= 37. 84 42

zdarzeń sprzyjających.  
Odpowiedź: 37 42

Wersja PDF